Summary

“Rethinking Progress” is an experimental work of electronic music in a format similar to that of a symphony. It consists of four instrumental parts (roughly corresponding to movements in a classical symphony) and a final song.

The symphony is not purely an audio piece. It comes with an official video synopsis. It is a philosophical tale of the past, present and future relationship between human beings and technology: from the naive idolization of “progress for the sake of progress” through a series of new discoveries and revolutions in human worldview, through attempts to escape from reality, to a true spiritual revolution that reshapes the human race.

The video combines the author’s original text and music with images that were created by other authors for purposes unrelated to this work, but parallel it aesthetically. This format was chosen to review the works of talented modern photographers and artists, and to support the freedom of quoting other authors' works in modern culture. All of the images were included under the fair use rule. Their authors are listed at the end of each part of the video.

The symphony’s melodies are simple and easy to understand, but together they form a unified, carefully thought-out system. Each symphony part plays at the same tempo of 120 beats per minute, and each instrumental part (including a pause at the end of each part) has a fixed duration of 192 measures, or 384 seconds. The final song plays for 256 measures, or 512 seconds. The overall length of the symphony is therefore 1024 measures, or 2048 seconds — just over 34 minutes. Each part of the symphony consists of four themes and some variations on them. Some of the melodies can be encountered in several parts, while others can only be found in one part. Each melody and harmony carries a specific meaning. This will be described in detail below, in the section “Melodic System of the Symphony”.

Each instrumental part is arranged in its own style:

• Part 1: techno.
• Part 2: NES chiptune.
• Part 3: pixel music (see description in the section “Pixel Music Concept”)
• Part 4: trance

The final song features all of these styles, though trance plays the dominant role. The symphony follows a carefully thought-out system of themes and their variations, which are described below in the section “Melodic System of the Symphony”.

The target audience of the “Rethinking Progress” symphony are people who are interested in melodic and experimental electronic music, transhumanist future studies, the philosophy of consciousness, ethics and religion, the psychology of altered states of consciousness, and science fiction in general.

The symphony was produced by the following people (on photos).

• Victor Argonov (music, arrangement, and text in parts 1-5). Music composer and scientist from Vladivostor, Russia. Founder of Victor Argonov Project and co-founder of Complex Numbers.
• Yelena Yakovets (vocals in part 5). Actress and singer from Vladivostok, Russia. The vocalist of Victor Argonov Project since 2003.
• Ariel (vocals in part 5). Singer from Vladivostok, Russia. Main vocalist of Victor Argonov Project since 2003 and Complex Numbers since 2004.
• Len (vocals in part 5). Singer, author, and art-manager from Ufa, Russia. Leader of the anime music cover project Harmony Team.
• Sayan Andriyanov (sound production in parts 1, 4, 5). Musician, doctor, and programmer from Novosibirsk, Russia. Leader of the Siberian ethnic rock band Bugotak.

English translation of synopsis was made by the following people.

• Adhal. Musician and linguist from Yuzhno-Sakhalinsk, Russia. Leader of the black metal band Kachangelion.
• Andrey Kopylov. Linguist from Sergiyev Posad, Russia.

Source files

Just like the operas, 2032: Legend of a Lost Future and The Little Mermaid, the Rethinking Progress symphony is going to come with detailed source files available freely for public use. Currently, however, only the MIDI files for all the parts are available, as well as the instrumental mix and two versions of the vocal track (“a cappella” versions) for part 5, Beyond the Line. These files can be used to create remixes. They can be accessed at https://gitlab.com/complexnumbers/reth-src. The name of each file contains the number of the symphony part it comes from, and a descriptor denoting the type of the file: “mid” for MIDI files, “voc” for vocal parts (“fin” for the edited vocal track with all the effects applied, and “raw” for the raw vocal track), and “ins” for the instrumental mix.

Melodic System of the Symphony

The symphony has nine basic musical themes, with the majority of them having several variations. All the themes are broken up into five rhythmic classes and can only use five chord progressions (see Figure 0). If two melodies are essentially the same and only differ by their chords, they are considered variations on the same theme.

Of the five chord progressions used in the symphony, three are minor, one is dominant, and one is major. On Figure 0, these progressions are color-coded: cold colors denote minor progressions, while warm colors denote major and dominant progressions. The progressions marked “blue” and “green” are trivial and are widely used in today’s culture. In this symphony they are used to express simple emotions. The other three, intended to express more complex emotions, have been intentionally borrowed from other works (cited in Figure 0) that show some similarities with the symphony in their style or aesthetics. Though Figure 0 shows these progressions in the key of C (or Am), they may be transposed to other keys, with their meaning staying unchanged.

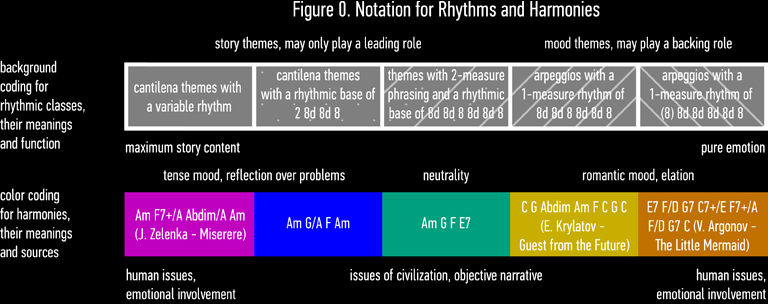
Each instrumental part of the symphony (parts 1-4) consists of four main themes (see Figure 1). The first theme is the “titular” theme (P, I, or C). Each part begins with this “titular” theme. The second theme is the main leitmotif of the symphony, M, which is present in all of its parts. The third theme is a “romantic” theme (D or S). The fourth theme is a syncopated arpeggio-based theme (T or A). Each instrumental part uses the “orange,” “yellow,” and “green” chord progressions. Parts 1 and 2 also use the “blue” progression, while parts 3 and 4 use the “magenta” progression.

The vocal part of the symphony (part 5) consists of four leading themes (cantilena themes: P, C, D, and L). Part 5 only uses three chord progressions: “blue”, “magenta,” and “orange”.

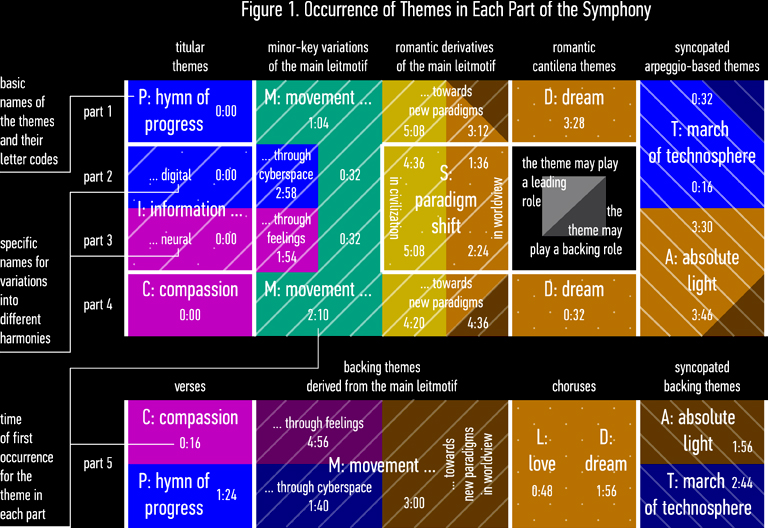
In this symphony, there is no division into primary, secondary, transitional, and closing themes, as is the case in the sonata form. However, there are some parallels with this system. The symphony emphasizes dialogue between harmonies rather than themes: the minor “blue” and “magenta” (tense, “problematic”) harmonies versus the dominant “orange” (“romantic”) one. The themes that play in the “blue” and “magenta” harmonies (P, I, C, T, and the “blue” and “magenta” variations of M) correspond to the primary themes in a classical sonata, while the themes that play in the “orange” harmony (L, D, A, and the “orange” variations of M and S) correspond to secondary themes. “Green” and “yellow” harmonies (“green” and “yellow” variations of M and S) play a “neutral” role.

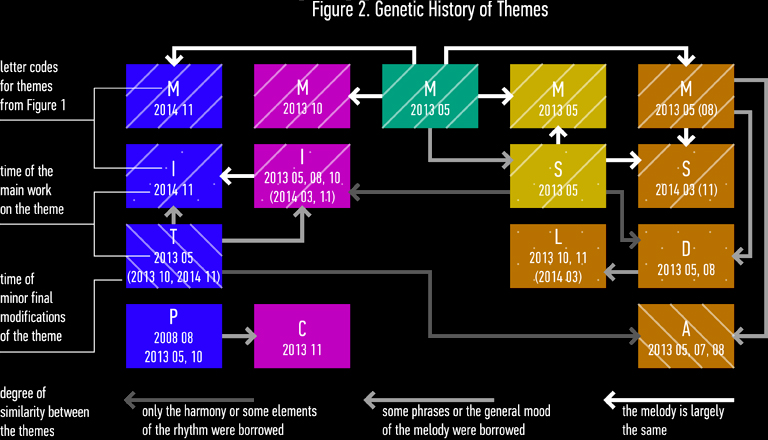
The themes' grouping by rhythmic class is based on the order in which they were composed (see Figure 2). The arpeggio-based themes T, A, and M have the simplest one-measure rhythms. These themes were among the first to be composed. They can either play the leading role or back the cantilena themes. I and S have a more complex rhythm. It is based on the rhythm of M, but every second measure is modified, so the melodies have a two-measure phrasing. The rhythm of the cantilena themes D and L is even more complex. It is based on S’s rhythm, but heavily modified. Because these themes have relatively few notes per measure, they can be sung, and in part 5 they serve as choruses. The other two cantilena themes — P and C — have been composed independently from all the other themes and have the most highly variable rhythm of them all. In part 5 they serve as verses.

Pixel synthesizer and Pixel Music Concept

Part 3 (“Constructing Sensations”) plays a unique role in the symphony, as it is arranged in the style of “pixel music”, an innovative style invented by the author.

Modern culture considers the sound of computers and gaming consoles of the 1980s — the NES, the Commodore 64, the Atari 8-bit computers, and the ZX Spectrum — to be the musical equivalent of pixel art. Many modern musicians simulate that sound and call it “chiptune” of “8-bit” sound. The key feature of the chiptune sound is that all waveforms have a discrete amplitude (generally the basic waveforms are 4-bit or even 1-bit, rather than 8-bit). The “square” shape of the waveforms can be likened to pixel art when seen in an oscilloscope. But this similarity is in fact quite superficial. An attempt to create a more rigorous musical equivalent of pixel art was made in “Constructing Sensations”.

Human hearing works in such a way that it perceives the spectrum of the sound (sonogram), but not the diagram of its amplitude over time (waveform). Since pixel art requires all features of the image to be visibly discrete (large pixels and a small number of colors), the pixel sound must likewise have a perfectly discrete sonogram. The pixel sound must meet the following principles.

• Principle 1. Discreteness in frequency. The signal is a sum of sine waves whose frequencies can only have a relatively small number of specific values. The frequencies of any two sine components must be easily distinguished by human ear (they must differ at least by a few percent).
• Principle 2. Discreteness in amplitude. The amplitude of each waveform can only have a small number of specific values. Any change in amplitude must be easily perceptible by human ear (the smallest possible rise or drop in volume must be of the order of a decibel).
• Principle 3. Discreteness in time. Any changes in spectrum (i. e. in the amplitudes of each constituent waveform) can only occur instantly at specific time moments. The interval between these moments must be constant and easily perceptible by human ear (no less than 1/20 of a second).

A perfect musical equivalent of pixel art must meet all three of these principles, while the majority of chiptune music only meets one of them — the discreteness in amplitude. The time is usually discrete as well, but the minimum step can be as small as 1/50 of a second, which is at the limit of the resolution of human hearing. The discreteness in frequency is usually absent, as the chiptune sound has a large number of harmonics that merge into indistinct noise in the upper part of the spectrum.

The vast majority of existing musical instruments cannot be used to implement the above principles. Some additive synthesizers do allow one to “assemble” the signal from a number of specific harmonics. For example, one could generate a sound consisting of six harmonics with the frequencies of 55, 110, 165, 220, 275, and 330 Hz with amplitudes of 6, 5, 4, 3, 2, and 1. However, the discreteness in amplitude disappears when one tries to change the volume of the signal. For example, if one cuts the signal’s volume in half, the amplitudes of harmonics 2, 4, and 6 would become fractions.

To deal with these difficulties, the author has created the specialized Pixel synthesizer (version 2016-12 beta). In this particular case, the principles of pixel music were applied in the following way.

• The sound of each note consists of sine waveforms whose frequencies correspond to the pitches of the tempered scale. Harmonics outside the scale (such as harmonics 7 or 14) are not allowed.
• Each waveform can have a discrete amplitude that ranges from 0 to 15.
• The amplitudes may change only at set points in time with the minimum interval being 32nd note.

In “Constructing Sensations” an additional restriction was put in place: no more than 12 notes may play at the same time. Most of these 12 voices were used for echoes or for long note decays (with small amplitudes of 1-3), so a total number of amplitude values used, even for bass sounds, were of the order of 30.

Principle 2 allows two alternative interpretations.

• Strong interpretation. There is a single standard set of possible amplitude values for all frequency components. For example, if a sine wave with a frequency of 55 Hz and a logical amplitude of 15 has an acoustic amplitude of -2 db, then a sine wave with any other frequency and the same logical amplitude of 15 must have the same acoustic amplitude of -2 db. No external equalizer (no spectral correction during mastering) can be used for such a track.
• Weak interpretation. Each frequency component has its own set of possible amplitude values. Two waveforms with the same logical amplitude but with different frequencies might have different acoustic amplitudes.

Both interpretations fit the idea of pixel music well, because any changes in the sound are easily perceptible by human ear. The strong interpretation looks better in technical terms, however, the weak one allows better optimization for human ear. In “Constructing Sensations,” the weak interpretation of Principle 2 was employed. For example, the signal in the 60-70 Hz range sounds 3 dB louder than the signal in the 200-300 Hz range with the same logical ampitude. This correction of spectrum was made during mastering in order to compensate for the uneven sensitivity of human hearing in different frequency ranges (and to make the track sound more similar to the other parts of the symphony). The raw version of “Constructing Sensations” without this adjustment (fitting the strong interpretation of Principle 2), can be downloaded here.

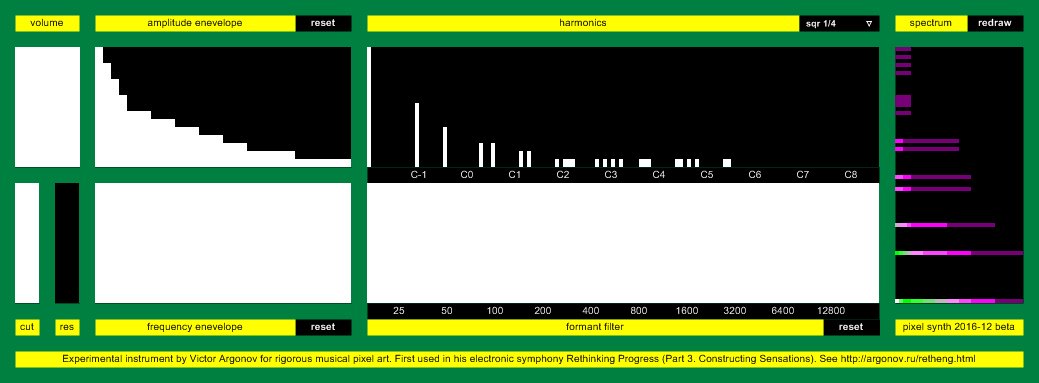
The image above shows how the Pixel synthesizer simulates the sound of a harpsichord. The upper middle window shows the spectrum of the original signal (not counting any changes over time). It includes harmonics that meet two criteria: (1) their number may not be multiple of 4 (which matches the spectrum of the asymmetric square wave in chiptunes, the so-called “pulse”), and (2) they must approximately correspond to pitches of the tempered scale (this makes the signal different from the “pulse”). Therefore, the signal’s spectrum consists of the following harmonics: 1 (C0), 2 (C1), 3 (G1), 5 (E2), 6 (G2), 9 (D3), 10 (E3), 15 (H3), 17 (C#4), 18 (D4), 19 (D#4), and so on. The amplitudes of the harmonics, just as in square waves, are inversely proportional to their numbers, but they may only take one of the 16 discrete values. The first harmonic has an amplitude of 15, the second one, 8, the third one, 5, the fifth and sixth ones, 3, and so on. The quality of this sound is very “ringing” and “metallic” (to a greater extent than the “pulse”). The upper left window plots the volume of the signal against time, with the time scale having 32 steps, corresponding to a measure of the musical composition. All alterations affect each harmonic independently. For example, the first harmonic changes its volume exactly as the graph shows, while upper harmonics that already have a volume of 1 play only for the first four steps, and then they just switch off. The large window to the right shows the changes in the spectrum of the output signal over time. The vertical axis shows the pitch of the note, while the horizontal axis shows time. The color of the line, ranging from black through blue, green, yellow, and white, shows the amplitude of the harmonic.As the image shows, the first harmonics to fade are the upper ones, which already play at a low volume. This gradual decay of harmonics is common for stringed instruments, but impossible for chiptunes.

The limited experience with the Pixel synthesizer that the author has acquired so far has shown that it does well at simulating the basic chiptune sounds — the symmetric and asymmetric 1-bit square waves, the 4-bit triangle wave, and some more traditional instuments as well, such as the organ, the harpsichord, and the bass guitar. The general quality of the sound is still different from that of chiptunes, being “clearer”, more “glassy” and less “thick”. The simulation of some percussion instruments raised many difficulties, as they either have a spectrum that covers all frequencies (such as the snare), or their volume changes quickly over time (such as the bass drum). The only percussion instrument that can currently be simulated in a satisfactory way is the hat.

Just like with any other technology, pixel music needs further refinement. New presets must be developed for the Pixel synthesizer, and new ways to use it must be found. The concept of pixel music may well turn out to be too experimental, and may occupy a very small niche. On the other hand, it may create a brand new style of music, just like chiptunes that have their own large audience.